베르누이 시행
베르누이 시행은 단 두가지 결과만을 가지는 실험이나 시행을 말한다. 이 두가지 결과는 일반적으로 "성공", "실패"
즉 1과0으로 구분되며, 각각의 확률은 p와 1-p이다. 여기서 p는 성공 확률을 나타낸다.

베르누이 시행의 대표적인 예로는 동전 던지기(앞면 또는 뒷면), 시험 합격여부(합격 또는 불합격)등이 있다.
이항분포
이항분포는 고정된 수의 n번의 독립적인 베르누이 시행에서 특정한 결과(성공)가 k번 나타날 확률 분포이다. 이 때, 각 시행의 성공 확률은 p로 동일하다. 이항분포의 확률 질량 함수는 아래와 같다.

이항분포의 예로는 10번의 동전 던지기에서 앞면이 나오는 횟수, 20명의 학생들 중 시험에 합격하는 학생의 수 등이 있다.
그래프로 보는 이항분포
이항분포의 모양은 n과 p에 따라 달라진다. 일반적으로, n이 커질수록, 그리고 p가 0.5에 가까울수록 분포는 더 대칭적이고 종 모양을 띠게 됩니다. 예를 들어, n=10이고 p=0.5인 이항분포는 아래 그림과 같다.
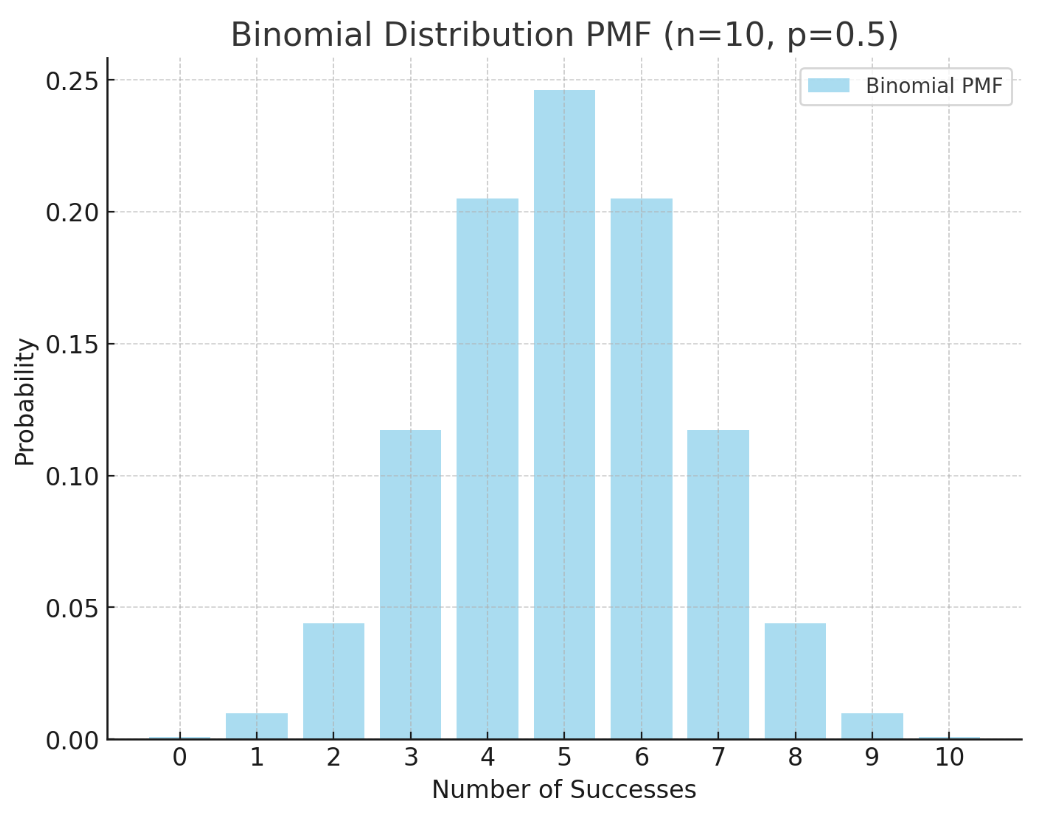
위 그래프는 n=10, p=0.5일 때의 이항분포를 나타낸다. 각 막대는 성공 횟수(k)에 대한 확률을 나타내며, 이 경우 동전을 10번 던졌을 때 앞면이 나올 횟수의 확률 분포를 보여준다. 분포는 대칭적이며, 가장 높은 확률은 k=5일 때, 즉, 10번 중 5번 성공(앞면이 나오는 경우)할 확률이 가장 높음을 알 수 있다.
이항분포는 각 시행이 독립적이며, 각 시행에서의 성공 확률이 일정할 때, 특정한 횟수의 시행에서 성공 횟수의 확률 분포를 나타내는데 효과적이다.
이항분포의 평균과 분산
이항분포의 평균(기대값)과 분산은 각각의 매개변수인 시행 횟수 과 성공 확률 에 의해 결정된다.
평균(기대값)
이항분포의 평균()은 전체 시행 횟수와 성공 확률의 곱으로 계산된다.
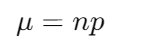
분산
이항분포의 분산()은 전체 시행 횟수, 성공 확률, 그리고 실패 확률의 곱으로 계산된다.
예를 들어, 시행 횟수 이고 성공 확률 인 이항분포의 평균과 분산을 계산해 보겠다.
시행 횟수가 이고 성공 확률이 인 이항분포의 경우 평균과 분산은 아래와 같다.

이항분포의 정규분포 근사
이항분포의 정규 근사는 큰 수의 이항분포가 정규분포로 근사될 수 있다는 개념이다. 이 근사는 중심극한정리의 한 예로, 시행 횟수 이 충분히 크고, 와 가 모두 충분히 큰 경우(일반적으로 각각 5보다 크다고 할 때) 이항분포는 평균 와 분산 를 가진 정규분포로 근사할 수 있다.
이항분포의 정규 근사 조건

근사 사용 예
이항분포의 정규 근사는 확률 계산을 단순화하기 위해 사용됩된다. 특히 이 큰 경우, 이항분포의 확률 질량 함수를 사용하여 확률을 직접 계산하는 것이 어렵거나 계산량이 많을 때 유용하다.
예를 들어, 이고 인 이항분포에서 특정 성공 횟수의 확률을 계산하려는 경우, 이 분포는 평균이 이고 분산이 인 정규분포로 근사할 수 있다.
근사의 한계
이항분포의 정규 근사는 근사이므로, 이 충분히 크지 않거나 가 0에 가깝거나 1에 가까운 극단적인 경우에는 부정확할 수 있다. 또한, 이항분포가 정규분포로 완벽하게 일치하지는 않으므로, 특히 꼬리 부분에서 차이가 발생할 수 있다.
이항분포의 정규 근사를 시각화하기 위해, 예를 들어 과 인 이항분포를 취하고, 이를 평균이 이고 분산이 인 정규분포로 근사해 보겠다. 이를 통해 이항분포와 정규분포의 형태를 비교할 수 있다.


위 그래프에서 파란색 점들은 n=100, p=0.5인 이항분포의 확률 질량 함수(PMF)를 나타낸다. 즉, 100번의 시행에서 특정 성공 횟수가 나올 확률을 보여준다. 반면에 빨간색 선은 이 이항분포를 정규분포로 근사한 것을 나타내는 확률 밀도 함수(PDF)이다. 이 근사는 평균이 50이고 표준편차가 5인 정규분포를 사용했다.
이 비교를 통해, n이 충분히 크고 p가 0과 1 사이에 있을 때, 이항분포는 정규분포로 잘 근사될 수 있음을 볼 수 있다. 특히, 그래프의 중심 부분에서 이항분포와 정규분포의 일치가 더욱 명확하며, 꼬리 부분에서는 약간의 차이가 나타날 수 있다.
'이론공부 > 통계' 카테고리의 다른 글
| 최소제곱법을 통한 회귀계수 행렬 구하기 (0) | 2024.04.09 |
|---|---|
| 불편추정량이란 (0) | 2024.04.09 |
| 척도의 종류 (1) | 2024.03.18 |
| [사회조사분석사] 통계분석과 활용 1-(1) (0) | 2024.03.04 |
| 선형회귀분석의 가정 (0) | 2023.02.24 |